线性表的查找：

一：顺序查找(线性查找)：

理解：顺序查找一个数据，找到该元素就返回其在数组中的下标，没找到则返回空。

优点：算法简单，逻辑次序无要求，且不同存储结构均适用。

缺点：ASL(平均查找长度)太长，时间效率低。

Demo：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import java.util.Scanner;
public class TestSequentialSearch {
	 	
	public static void main(String[] args) {
		int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,};
		System.out.println("请输入要查询的数字：");
	 	Scanner input=new Scanner(System.in);	
	 	int input1=input.nextInt();	
	 	SequentialSearch(a,input1);
		
	}
	public static void SequentialSearch(int[] arr,int input){
		
	 	for(int i=0;i<arr.length;i++){
	 		if(arr[i]==input){
	 			System.out.println(input+"的位置为："+i);	
	 			break;
	 			}
	 		if(i==arr.length-1)
	 			System.out.println("No Result!");
	 		}
	 	} 
}

时间复杂度：O(n)

空间复杂度：O(1)

小Tips：可以添设”哨兵“，来加快速度。

二：折半查找(二分或对分查找)：

理解：得到首元素的索引head，并求出数组长度length-1得到尾元素的索引end。利用首尾元素求出中间元素middle， [ (head + end) / 2 ] ,利用middle值与target值进行比较，如果相同，则返回。如果不同,middle>target，则进行尾元素索引的更改,变为end=middle-1；如果middle<target，则进行首元素索引的更改,变为head=middle+1；

优点：效率比顺序查找高。

缺点：只适用于有序表，且限于顺序存储结构(对线性表无效)。

Demo：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class SearchUtils {
    public static void main(String[] args) {
        SearchUtils su = new SearchUtils();
        int[] arr = {1,3,6,9,12,23,33,44,45,67,78,98,100};
        int res = su.binarySearch(arr, 44);
        System.out.println("res=" + res);
    }

    public int binarySearch(int[] arr, int target) {
        int head = 0;
        int end = arr.length - 1;
        int middle;
        while (head <= end) {
            middle = (head + end) / 2;
            //如果要查找的元素target小于中间位置的元素middle，指向数组的较大端的end索引重新指向中间索引middle的左边（middle-1）
            if (target < arr[middle]) {
                end = middle - 1;
            }
            //如果要查找的元素target大于中间位置的元素middle，指向数组的较小端的head索引重新指向中间索引middle的右边（middle+1）
            if (target > arr[middle]) {
                head = middle + 1;
            }
            if (arr[middle] == target) {
                return middle;
            }
        }
        return -1;
    }

}

时间复杂度：O(lg2^n)

三：分块查找(索引顺序表的查找)：

理解：先将所有元素按大小进行分块，然后在块内进行查找。在分块时，块内的元素不一定是有序的，只要一个块内的元素在同一区间就行。用标准的语言描述是：算法的思想是将n个数据元素”按块有序”划分为m块,(m ≤ n)。每块中的关键字（元素）不一定有序，但前一块中的最大关键字必须小于后一块的最小关键字，即要求表示“分块有序”的。

思想：首先查找索引表，因为索引表为有序表，所以可以利用顺序或折半查找，再在块内进行查找，因为块内可以无序，所以利用顺序查找，在块内查找到则显示查询成功，否则查找失败。

e.g：索引表：

14 34 66
0 5 10

元素表：

索引 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
值 8 14 6 9 10 22 34 18 19 31 40 38 54 66 46

查找过程：先确定待查记录所在块(顺序或折半查找),再在块内查找(顺序查找)。

查找效率：ASL=Lb（对索引表查找的ASL）+Lw（对块内查找的ASL）

优点：插入删除比较容易，无需进行大量移动。

缺点：要增加一个索引表的存储空间并对初始化索引表并对初始索引表进行排序运算。

适用情况：如果线性表既要快速查找又经常动态变化，则可采用分块查找。

Demo：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
public class SSTable {

    private int data[];
    private int length;
    public int searchIndex(IndexTable it, int m, SSTable st, int n, int k) {
        int low = 0, high = m -1, mid, i;
        int b = n/m;
        while (low <= high) {
            mid=(low + high) / 2;
            if (it.elem[mid].key >= k) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }

        if (low < m) {
            i = it.elem[low].start;
            while (i <= it.elem[low].start + b -1 && st.data[i] != k) {
                i++;
            }
            if (i <= it.elem[low].start + b -1){
                return i;
            } else {
                return -1;
            }
        }

        return -1;
    }

    public void  createSSTable(int[] a){
        this.data = new int[a.length];
        for (int i = 0; i < a.length; i++) {
            this.data[i] = a[i];
            this.length++;
        }
    }

    /* 索引表结点 */
    public class IndexItem {
        public  int key;
        public  int start;
    }

    /* 索引表 */
    public class IndexTable{
        public  IndexItem[] elem;
        public int length = 0;
        public void createIndexTable(int[][] b){
            this.elem = new IndexItem[b.length];
            int i;
            for (i = 0; i < b.length; i++){
                elem[i] = new IndexItem();
                elem[i].key = b[i][0];
                elem[i].start = b[i][1];
                this.length++;
            }
        }
    }

    public static void main(String[] args) {
        int[] a = {8, 14, 6, 9, 10, 22, 34, 18, 19, 31, 40, 38, 54, 66, 46};
        int[][] b = {{14, 0},{34, 5},{66, 10}};
        SSTable st = new SSTable();
        IndexTable it = st.new IndexTable();
        st.createSSTable(a);
        it.createIndexTable(b);
        int x = st.searchIndex(it, b.length, st, a.length, 10);
        if (x < 0) {
            System.out.println("要查找的元素不存在");
        } else {
            System.out.println("查找成功，该元素在表中的位置为：" + (x + 1));
        }
    }

}

数表的查找：

  • 当表插入、删除等操作频繁时，为维护表的有序性，需要移动表中很多记录。

改用动态查找表—几种特殊的树

  • 表结构在查找过程中动态生成。

  • 对于给定值key，若表中存在，则成功返回；否则，插入关键字等于key的记录。

1：二叉排序树：

  • 又称二叉搜索树，二叉查找树。

定义：

二叉排序树或是空树，或是满足如下性质的二叉树：

  1. 若其左子树非空，则左子树上所有结点的值均小于根结点的值;
  2. 若其右子树非空，则右子树上所有节点的值均大于根节点的值;
  3. 其左右子树本身又各是一颗二叉排序树;

中序遍历非空的二叉排序树所得到的数据元素序列是一个按关键字排列的递增有序序列。

查找：
  • 若查找的关键字等于根节点，成功。
  • 否则
    • 若小于根节点，查其左子树。
    • 若大于根结点，查其右子树。
  • 在左右子数上的操作类似。

进阶思想：二叉排序树的递归查找

  1. 若二叉排序树为空，则查找失败，返回空指针。
  2. 若二叉树排序树非空，则给定值key与根节点的关键字。
  • 若key等于根结点，则查找成功，返回根节点地址。
  • 若key小于根结点，则进一步查找左子树。
  • 若key大于根节点，则进一步查找右子树。

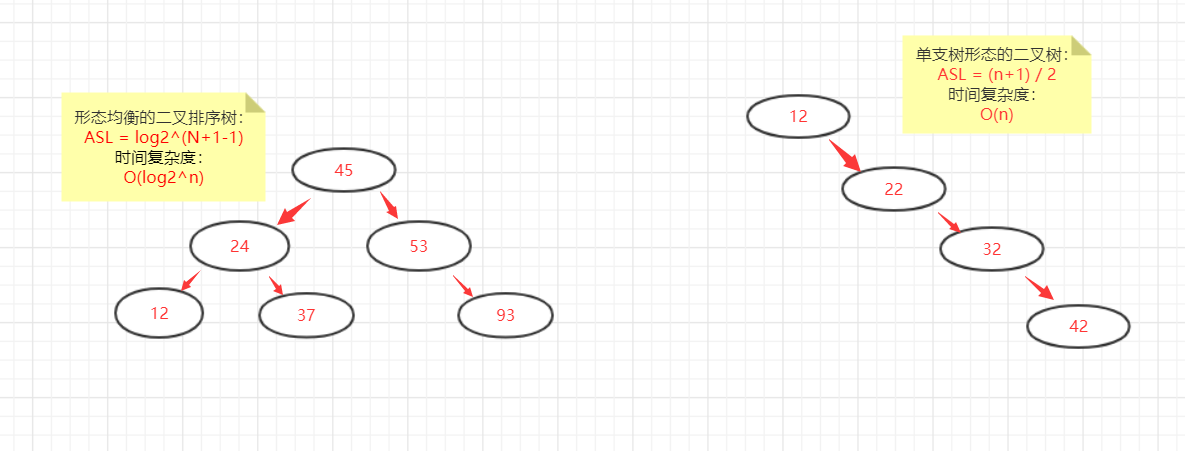
二叉树排序树的查找分析：

二叉排序树上查找某关键字等于给定值的结点过程，其实就是走了一条从根到该结点的路径。

  • 比较的关键字次数=此节点所在层次数
  • 最多的比较次数=树的深度
  • 含有n个结点的二叉排序树的平均查找长度和树的形态有关。
  • 尽量让二叉树的形态均衡，提高二叉排序树的查找效率。

插入：
  • 若二叉排序树为空，则插入结点作为根节点插入到空树中。
  • 否则，继续在其左、右子树上查找
    • 树中已有，不再插入
    • 树中没有
      • 查找直至某个叶子结点的左子树或右子树为空为止，则插入结点应为该叶子结点的左孩子或有孩子。

通俗一点的说法就是：

①：如果空，则为根节点。

②：大于根结点，插入右子树。

③：小于根结点，插入左子树。

二叉排序树的操作：—生成：

  • 从空树出发，经过一系列的查找、插入操作之后，可生成一棵二叉排序树。
  • 一个无序列序列可通过构造二叉排序树而变成一个有序序列。构造树的过程就是对无序序列进行排序的过程。
  • 插入的结点均为叶子结点，故无需移动其他结点。相当于在有序序列上插入记录而无需移动其他记录。

但是：

  • 关键字的输入顺序不同，建立的二叉树排序树不同。
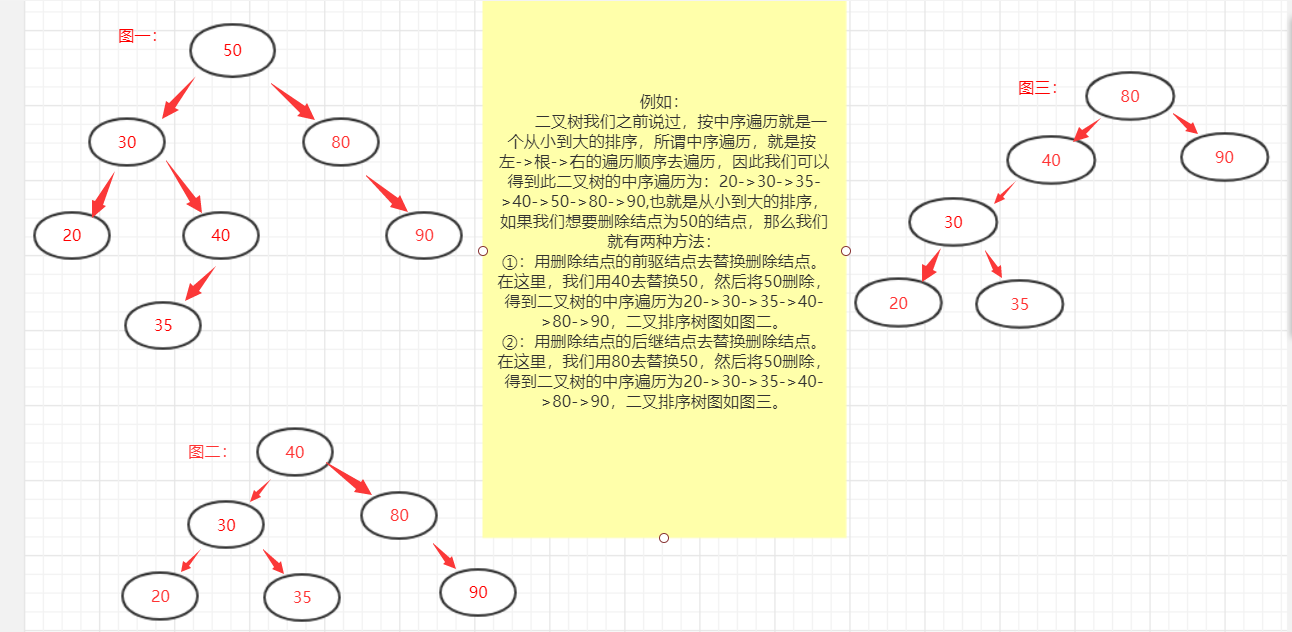
删除：

关于删除，相对来说要比查找和插入要麻烦一些，但是请耐心看下去。

  • 从二叉排序树中删除一个结点，不能把以该结点为根的子树都删去，只能删除该结点，并且还应保证删除后所得的二叉树仍然满足二叉排序树的性质不变。
  • 由于中序遍历二叉排序树可以得到一个递增有序的序列。那么，在二叉排序树中删去一个结点相当于删去有序序列中的一个结点。
    • 将因删除结点而断开的二叉链表重新连接起来。
    • 防止重新链接后树的高度增加。

通俗一点的说法就是：

①：被删除的为叶子结点，直接删去该结点。

②：被删除结点只有右孩子或左孩子，用其左子树或右子树替换它(结点替换)。其双亲结点的相应指针域的值改为”指向被删除结点的左子树或右子树”。

③：被删除的节点上既有左子树，又有右子树：

  • (1)：用前驱结点去替换，然后删除要删除的结点。
  • (2)：用后继结点去替换，然后删除要删除的结点。
  • 不管用前驱结点替换还是后继结点替换，都应该保存二叉树的性质;

Demo：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
    public class BinaryTree {

        /**
         * BinaryTree 的节点数据结构
         */
        private class TreeNode{
            private int key = 0;
            private String data = null;
            private boolean isVisited = false;
            private TreeNode leftChild = null;
            private TreeNode rightChild = null;

            public TreeNode(){}
            public TreeNode(int key,String data){
                this.key = key;
                this.data = data;
                this.leftChild = null;
                this.rightChild = null;
            }
        }

        //获取根节点
        public TreeNode getRoot() {
            return root;
        }

        public void setRoot(TreeNode root) {
            this.root = root;
        }


        //定义根节点
        private TreeNode root = null;
        public BinaryTree(){
            root = new TreeNode(10,"A");
        }

        /**
         * 创建一棵二叉树
         */
        public void createBinaryTree(TreeNode root){
            TreeNode nodeB = new TreeNode(8,"B");
            TreeNode nodeC = new TreeNode(12,"C");
            TreeNode nodeD = new TreeNode(7,"D");
            TreeNode nodeE = new TreeNode(9,"E");
            TreeNode nodeF = new TreeNode(22,"F");
            root.leftChild = nodeB;
            root.rightChild = nodeC;
            nodeB.leftChild = nodeD;
            nodeB.rightChild = nodeE;
            nodeC.rightChild = nodeF;

        }

        /**
         * 前序遍历
         */
        public void preOrder(TreeNode node){
            if(node != null){
                visited(node);
                preOrder(node.leftChild);
                preOrder(node.rightChild);
            }
        }
        /**
         * 中序遍历
         * @param node
         */

        public void inOrder(TreeNode node){
            if(node != null){
                preOrder(node.leftChild);
                visited(node);
                preOrder(node.rightChild);
            }
        }
        /**
         * 后序遍历
         * @param node
         */

        public void postOrder(TreeNode node){
            if(node != null){
                preOrder(node.leftChild);
                preOrder(node.rightChild);
                visited(node);
            }
        }
        /**
         * 非递归前序遍历
         * @param node
         */

        public void nonRecPreOrder(TreeNode node){
            Stack<TreeNode> stack = new Stack<>();
            TreeNode pNode = node;
            while(pNode != null || stack.size()>0){
                while(pNode != null){
                    visited(pNode);
                    stack.push(pNode);
                    pNode = pNode.leftChild;
                }
                if(stack.size()>0){
                    pNode = stack.pop();
                    pNode = pNode.rightChild;
                }
            }
        }
        /**
         * 非递归中序遍历
         * @param node
         */

        public void nonRecInOrder(TreeNode node){
            Stack<TreeNode> stack = new Stack<>();
            TreeNode pNode = node;
            while(pNode != null || stack.size()>0){
                while(pNode != null){
                    stack.push(pNode);
                    pNode = pNode.leftChild;
                }
                if(stack.size()>0){
                    pNode = stack.pop();
                    visited(pNode);
                    pNode = pNode.rightChild;
                }
            }
        }

        /**
         * 非递归后序遍历
         * @param pNode
         */
        public void nonRecPostOrder(TreeNode pNode){
            Stack<TreeNode> stack = new Stack<>();
            TreeNode node = pNode;
            while(pNode != null){
//左子树入栈
                while(pNode.leftChild != null){
                    stack.push(pNode);
                    pNode = pNode.leftChild;
                }
//当前节点无右子树或者右子树已输出
                while(pNode != null && (pNode.rightChild == null || pNode.rightChild == node)){
                    visited(pNode);
//记录上一个已输出的节点
                    node = pNode;
                    if(!stack.isEmpty()){
                        pNode = stack.pop();
                    }else{
                        return;
                    }
                }
//右子树入栈
                stack.push(pNode);
                pNode = pNode.rightChild;
            }
        }

        private void visited(TreeNode node) {
            node.isVisited = true;
            System.out.println(node.data+","+node.key);
        }

        /**
         * 计算树的高度
         */
        private int height(TreeNode node){
            if(node == null){
                return 0;
            }else{
                int i = height(node.leftChild);
                int j = height(node.rightChild);
                return (i<j)?j+1:i+1;
            }
        }

        /**
         * 计算树的节点数
         * @param node
         * @return 树的节点数
         */

        private int size(TreeNode node){
            if(node == null){
                return 0;
            }else{
                return 1+size(node.leftChild)+size(node.rightChild);
            }
        }



        public static void main(String[] args) {
            BinaryTree binaryTree = new BinaryTree();
            TreeNode root = binaryTree.root;
            binaryTree.createBinaryTree(root);
            System.out.println(binaryTree.height(root));
            System.out.println(binaryTree.size(root));
            binaryTree.preOrder(root);
            System.out.println("*******");
            binaryTree.nonRecPreOrder(root);
            System.out.println("*******");
            binaryTree.nonRecInOrder(root);
            System.out.println("-------------");
            binaryTree.nonRecPostOrder(root);
        }

    }

2：平衡二叉树：


2021-04-09