BCD码:
4个二进制位 (4bit) —-> 1个十进制位,又因为4个二进制位有2的4次方种状态,也就是16种状态。
16种状态足够表示十进制的0~9,并且还有6种冗余。
8421码:
8421码的映射关系:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 |
8421码在计算机中进行加法运算:
十进制: 5 + 8 =13
8421码: 0101 + 1000 =1101
因为1101不再映射表里,所以需要加上冗余的6,也就是0110
所以1101+0110=1 0011
0011在映射表里为3,在高位的1前面补0为0001
所以0001 0011在映射表里为13
注:若相加结果在合法范围内,则无需修正。(因为8421码的二进制位的权值是固定不变的8421,所以8421码也成为有权码)
余3码:
余3码映射表:( 8421码 + 0011 (二进制) )
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 |
- 余3码的四个二进制每一个二进制没有固定的权值,所以余3码也成为无权码
2421码:
2421码映射表:(与8421码不同是改变了权值的定义)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0000 | 0001 | 0010 | 0011 | 0100 | 1011 | 1100 | 1101 | 1110 | 1111 |
2421码的二进制权值是固定的2421,也是有权码
对于2421码来说,0~ 4范围内所有数字编码的第一位都为0,5~ 9范围内所有的数字编码的第一位都为1
上述的规定第一位是为了避免歧义,例如5可以表示为0101或1011,但规定了数字编码的第一位后就不会存在歧义。
字符:
ASCII码:
数字、字母、符号共128个字符—>7位二进制编码
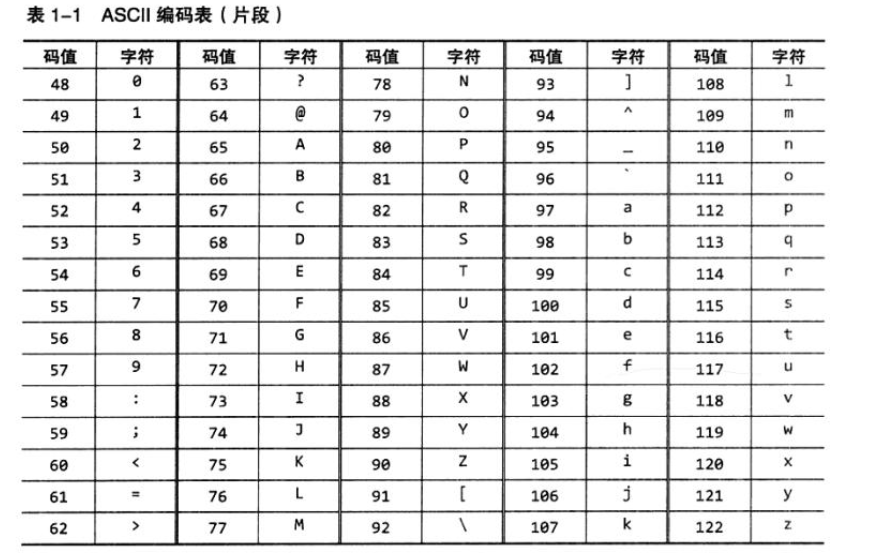
可印刷字符:32~126
数字:48(011 0000)~57(011 1001)
大写字母:65(100 0001)~90(101 1010)
小写字母:97(110 0001)~122(111 1010)
例:已知’A’的ASCII码的值为65,字符’H’存放在某存储单元M中,求M中存放的内容。
**注意:M中存放的是‘H’的ASCII码(二进制形式)**。
一:A是第一个字母,H是第8个字母,则H对应的码值=65+(8-1)=72;72对应二进制为100 1000,故M中存放的内容为0100 1000
二:A的码值65写成二进制为100 0001,A是第一个字母,H是第八个字母,故对应100 1000,M中存放的内容为0100 1000。
每个存储单元存放的内容为字节(Byte)的整数倍,即8的整数倍,例题假设存放1B。
字符串:
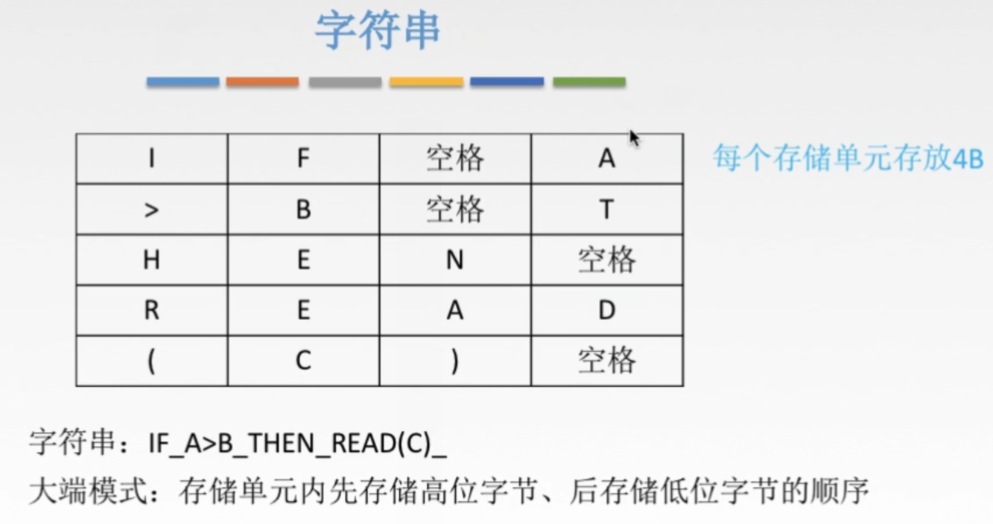
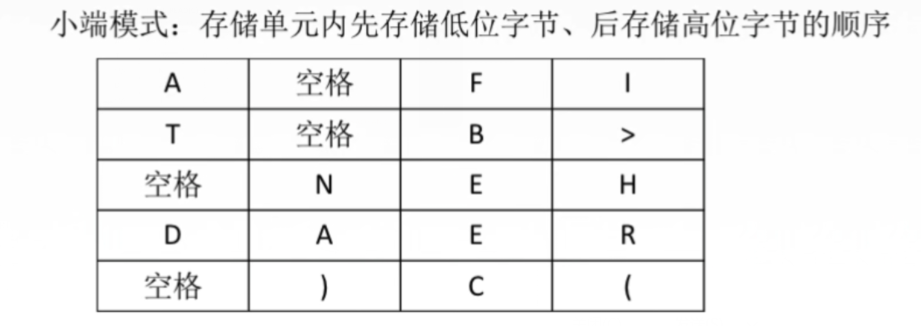
汉字的表示和编码:
GB 2312-80:汉字+各种符号共7445个
区位码:94个区,每区94个位置
例如:啊,在第16区,01位置。
将16转换为十六进制为10H,01转换为十六进制为01H,但是为了防止与其它编码冲突,所以在
16进制的基础上再加上20H,变成30H和21H.这就是国标码,但会与ASCII码冲突,所以再加上80H得到B0H和A1H,这就是汉字计内码,完成汉字在计算机中的存储。
奇偶校验码:
信息 A B 码字 00 01 码距1 码字(方案二) 00 11 码距2 码距:两个合法码字对应位上数字的不同的个数
例如:原本A(00)因为跳变发送到B变成了(01),但因为码距为1,所以无法判断原本发的数据是正确还是错误。
而A(00)因为跳变变成了01,但码距为2,可以知道发生了错误,因为没有01,但却无法确定是哪一位发生了跳变。所以在整个方案中,有些编码是我们没有用到的,没有用到的编码在发生错误的时候可以帮我们指示错误原因。
奇校验码:整个校验位(有效信息位和校验位)中1的个数为奇数。
偶校验码:整个校验位(有效信息位和校验位)中1的个数为偶数。
奇偶校验位 有效信息位 1位 n位 海明码:
海明码设计思路:
分组校验-->多个校验位-->校验位标注出错位置。例如:信息位1010
因为:2的K次方 ≥ n+k+1
所以:K = 3;
对于n+k+1:海明码是检验信息中哪一位出错,所以原码n个,检验码k个,出现n+k个位置,k校验码对应2的k次方个状态,如k=3,对应000~ 111八个状态。如果八个状态都为错误状态,就需要一个表示正确状态,所以为n+k+1。
1:设信息位D4 D3 D2 D1(1010)共4位,检验位P3 P2 P1,共3位,对应的海明码为H7 H6 H5 H4 H3 H2 H1。
2:确定校验位的分布
H7 H6 H5 H4 H3 H2 H1 D4 D3 D2 P3 D1 P2 P1 1 0 1 0 0 1 0 第二行校验位Pi放在海明码为2的(i-1)次方的位置上,信息位按顺序防到其余位置。
3:求校验位的值:
H3:3—>0 1 1
H5:5—>1 0 1
H6:6—>1 1 0
H7:7—>1 1 1
按列看,最左边的列1 1 0 1说明H3 H5 H7不为0,因此用D1 D2 D4进行异或得P1—>0
第二列1 0 1 1说明H3 H6 H7不为0,因此用D1 D3 D4进行异或得P2—>1
第三列0 1 1 1说明H5 H6 H7不为0,因此用D2 D3 D4进行异或得P3—>0
4:纠错
校验方程:
S1=P1⊕D1⊕D2⊕D4
S2=P2⊕D1⊕D3⊕D4
S3=P3⊕D2⊕D3⊕D4
接收到:1010010
S1=P1⊕D1⊕D2⊕D4 = 0⊕0⊕1⊕1=0
S2=P2⊕D1⊕D3⊕D4 = 1⊕0⊕0⊕1=0
S3=P3⊕D2⊕D3⊕D4 = 0⊕1⊕0⊕1=0
000无错误。
接收到:1010000
S1=P1⊕D1⊕D2⊕D4 = 0⊕0⊕1⊕1=0
S2=P2⊕D1⊕D3⊕D4 = 0⊕0⊕0⊕1=1
S3=P3⊕D2⊕D3⊕D4 = 0⊕1⊕0⊕1=0
010转换为二进制为2,则第2位出错,该为1010010
(格式如果变化,确定校验位得分布摆放位置变化,计算方法不变)
CRC循环冗余码:
| 信息位 | 校验位 |
|---|---|
| K位 | R位 |
例:设生成多项式为G(X) = x的三次方+X的2次方+1,信息码为101001,求对应的CRC码
1:确定K,R以及生成多项式对应的二进制码。
K = 信息码的长度 = 6,R = 生成多项式最高次幂 = 3 –> 校验码位数N = K+ R =9
生成多项式G(X) = 1·(X^3)+1·(X^2)+0·(X^1)+1·(X^0),对应的二进制码1101
2:移位:
信息码左移R位,低位补0 —–> 1101000
3:相除(模2除):
对移位后的信息码,用生成多项式进行模2除法,产生余数
1101000 / 1101
模2除:看被除数的最高位是1还是0,根据最高位去上位。减法做不带进位的减法,进行异或运算(相同为0,不同为1),最终取得的余数为校验位。对应的CRC码就是信息码+校验位。

4:检错和纠错:
例:发送:101001001 记为C9C8C7C6C5C4C3C2C1
接收:101001001—–>用1001进行模2除—->余数000,代表没出错。
接收:101001011—->用1101进行模2除—->余数为010,二进制转换为2,C2出错,但不是绝对,因为000只能代表8位,并不能完全表示。
| 原循环冗余码 | 出错一位后的循环冗余码 | 出错位 | 余数 |
|---|---|---|---|
| 101001 001 | 101001 000 | 1 | 001 |
| 101001 011 | 2 | 010 | |
| 101001 101 | 3 | 011 | |
| 101000 001 | 4 | 100 | |
| 101011 001 | 5 | 101 | |
| 101101 001 | 6 | 110 | |
| 100001 001 | 7 | 111 | |
| 111001 001 | 8 | 001 | |
| 001001 001 | 9 | 010 |
假设信息位是K,校验位是R,那么CRC的位数就是R + K ,而R的校验位,可以表示的数从0到2R-1,而0用来表示正确的情况,那么一共有2R-1种错误码,其中每个错误码对应一位,因此我们可以得到一个公式,当满足2R - 1 >= K+R的时候,CRC才具有纠错功能。而且我们可以发现余数是每7个一个循环,出错位1和出错位8的余数是一样的,出错位2和出错位9的余数是一样的,所以这也是为什么叫做循环冗余码的原因。
为什么一般我们不提及CRC的纠错功能,因为CRC一般用在计算机网络中,在以太网的MAC帧中,通常4字节的效验码(FCS)不但用来检验MAC帧的数据部分,还用来检验目的地址、原地址和类型字段(60~1514)字节,信息位远远大于校验位,因此我们一般不提及CRC的纠错功能,但这并不代表没有。